S1.4 Mole Calculations
Mole and Particles:
The mole (mol) is the SI unit for the amount of substance. One mole contains exactly 6.022 × 10²³ elementary entities such as atoms, molecules, or ions. This number is known as Avogadro’s number and allows chemists to count particles by weighing them. The amount of substance is usually represented by the symbol n, and its unit is the mole (mol).
n = N
Na
n = Number of Moles
N = Number of Particles
Na = Avogadro's Number (6.022 x 10^23 mol)
Worked Example:
How Many Mols are in 3.011 x 10 ^23 molecules of CO2
Solution:
n = N
Na
n = 3.011 x 10^23
6.022 x 10^23
n = 0.5 Mols
Mole and Mass:
n = m
M
n = Number of Moles
m = mass (grams)
M = Molar Mass (g/mol)
Worked Example:
What is the number of Moles in 20g of NaOH?
Solution:
Using the periodic table, the molar mass of Na is 22.99 g/mol and O is 16.00 g/mol and H is 1.01g/mol
Therefore Molar mass of NaOH is:
M(NaOH) = 22.99 + 16.00 + 1.01 = 40 g/mol
n = m
M
n = 20 grams
40 g/mol
n = 0.5 Mols
Mole and Concentration:
n = C x V
n = Number of Moles
C = Concentration ( mol.dm^-3 )
V = Volume (dm^3)
Worked Example:
Calculate the concentration of a solution with 2 moles of a solute dissolved in a 0.5 dm^3 solution
Solution:
n = C x V
C = n
V
→
C = 2 moles
0.5 dm^3
C = 4 Mols.dm^-3
Mass Concentration:
m = mass (g)
C = Concentration ( g.dm^-3 )
V = Volume (dm^3)
C = m
V
Worked Example:
what is the concentration (g/dm^3) of a solution with 10g of NaCl in 0.5 dm^3
Solution:
C = m
V
C = 10 grams
0.5 dm^3
C = 20 g.dm^-3
Density:
ρ = density (g/cm^3 or Kg/m^3)
m = mass (g)
V = Volume (cm^3 or m^3)
ρ = m
V
Worked Example:
what is the density of a solution with a mass of 100 grams and volume of 250 cm^3
Solution:
ρ = m
V
ρ = 100 grams
250 cm^3
ρ = 0.4 g/cm^3
Molarity from Mass Concentration:
ρi = mass concentration (g/dm^3)
M = molar mass (g/mol)
C = Concentration (mol/dm^3) (Molarity)
C = ρ
M
Worked Example:
A solution has a mass concentration of 36.5 g/dm^3. what is the molarity if the solute is HCl (M=36.5 g/mol)
Solution:
C= ρ
M
C = 36.5 g/dm^3
36.5 g/mol
C = 1 mol/dm^3
What is the difference between density, mass concentration and molar concentration?
Density, mass concentration, and molar concentration are related concepts used in different contexts. Density refers to how much mass is contained in a given volume of a pure substance and is a general physical property. Mass concentration describes how much solute is dissolved in a specific volume of solution, focusing on mixtures rather than pure substances. Molar concentration, on the other hand, expresses the amount of solute in moles per volume of solution and is essential for understanding chemical reactions and stoichiometry. While these concepts may appear similar, each serves a distinct purpose depending on whether you're dealing with pure substances or solutions.
Clarification !
Dilution:
C1 x V1 = C2 x V2
Dilution is the process of reducing the concentration of a solution by adding more solvent (usually water)
C = Concentration (mol/dm^3)
V = Volume (depends on the unit given in context)
NOTE : Dilution does not change the number of moles of solute; it only increases the volume of the solution, which decreases the concentration.
Worked Example:
What volume of a 2 mol/dm^3 HCl is needed to make a 100 cm^3 of 0.5 mol/dm^3 solution?
Solution:
C1 x V1 = C2 x V2
2 x V1 = 100 x 0.5
2 x V1 = 50
V1 = 25 cm^3
Empirical and Molecular Formulas:
The empirical formula is the simplest whole number ratio of atoms in acompound1. Steps to determine the EF from percentage composition:
-
Assume 100 g of the compound (so % → g)
2. Convert mass of each element to moles using: moles = mass (g) / molar mass (g/mol)
3. Divide all mole values by the smallest mole value.
4. Round to the nearest whole number (if needed, multiply all values to get whole numbers).
Note: the Empirical Formula shows the simplest ratio of atoms of each element in a molecule. While the molecular formula the actual number of atoms of each element in a molecule
Worked Example:
A molecule is shown to be composed of 40% carbon, 6.7% hydrogen and 53.3% oxygen. determine its empirical formula.
Solution:

Worked Example:
Determine the same molecules molecular formula, when the molar mass of the molecule is (M=180 g/mol)
Solution:
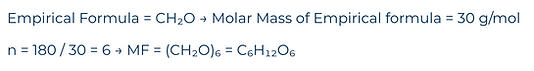
Avogadro's Law
The law states "at constant temperature and pressure, equal volumes of gasses contain equal number of moles (particles)"
n1
n2
V1
V2
=
n = number of moles
v = volume (dm^3)
Worked Example:
Two samples of gas are measured at the same temperature and pressure. Sample A contains 1.5 moles of oxygen gas and occupies 33.6 dm^3 of space. What volume would 2.5 mol of the same gas occupy under the same conditions.
Solution:
V2 = 56 dm^3
n1
n2
V1
V2
=
1.5
2.5
33.6
V2
=
