S1.3 Electron Configuration
1.3.1: Emission Spectra
When an element is heated or subjected to high voltage, its atoms absorb energy, exciting theelectrons to higher energy levels. As these electrons return to their lower, more stable states, they release energy in the form of light. This light, when passed through a prism, forms an emission spectrum: a series of bright, colored lines on a dark background.

Each element emits a unique pattern of spectral lines, acting like a fingerprint. These patterns provided the first evidence that:
1. Electrons exist in specific energy levels (quantized).
2. Electrons transition between fixed orbits, not randomly.
3. The energy released (and hence the wavelength of light emitted) corresponds to thedifference between energy levels.
1.3.2 & 1.3.3: Hydrogen Bond
When electrons in a hydrogen atom absorb energy, they move to higher energy levels (excited states). As they return to lower energy levels, they emit photons. These photons produce specific wavelengths of light that appear as bright lines on a dark background, this is the emission spectrum of hydrogen.
Each line in the spectrum corresponds to a transition between two energy levels. The final level(lower level) determines the series the transition belongs to
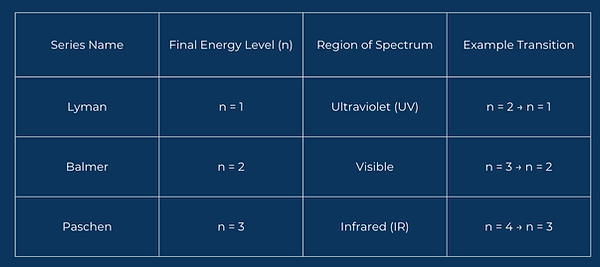

As the energy levels get higher (e.g., n = 6, 7, 8...), the lines in the emission spectrum get closer together—this is called convergence. The lines converge at a specific point called the convergence limit. Beyond this point, the electron has enough energy to escape the atom completely → the atom is ionized. This confirms that energy levels are not infinite, but they get closer together as n increases, and they eventually merge.
Application
Pull Up your Calculators, Data Booklets and Brains
Formulas & Constants Needed (Section 1&2 of the data Booklet )
Speed of Light (C) = 3.00 × 108 m s−1
Planks Constant (h) = 6.63 × 10-34 J s
C= λ ×f→ (λ=wavelength & f = frequency)
Energy of Photon: E = h × f
Worked Example:
A beam of light has a wavelength of 5.00 × 10−7 m. Calculate the energy of a single photon? Use:
Solution:
f = C / λ
f = 3.00 × 108 m s−1 / 5.00 × 10−7 m
= 6 x 10^14 Hz
E = h x f
E = (6.63 x 10^-34) x (6 x 10^14)
= 3.978×10⁻^-19 J
1.2.4: The Quantum Mechanical Model
The quantum mechanical model is the most accurate and widely accepted model of the atom. It states that electrons are found in orbitals. Orbitals are regions of space where there's a high probability of finding an electron. It also states that energy levels are quantified: Electrons occupy discrete energy levels, just like in the Bohr model, but now within sublevels and orbitals (s, p, d, f).
Drawing Skills

1.3.5: Electron Configuration
Electron configuration is a method of showing how electrons are distributed among the orbitals of an atom. Electrons occupy energy levels (shells), which are divided into sublevels:
- s: 1 orbital, holds up to 2
- p: 3 orbitals, holds up to 6
- d: 5 orbitals, holds up to 10
- f: 7 orbitals, holds up to 14
An electron configuration can be written in:
Standard form: listing all filled orbitals.
Condensed form: using the previous noble gas in brackets to shorten the notation.
Example - Oxygen (z = 8)
- Full configuration: 1s² 2s² 2p⁴
- Condensed configuration: [He] 2s² 2p⁴
Atomic Orbitals:
Orbital diagrams are a visual representation of how electrons are arranged within atomic orbitals. Unlike electron configuration notation, which lists the number of electrons per sublevel (e.g.,2p⁴), orbital diagrams show the individual orbitals and the electrons in them, including their spins.
- Each orbital is represented by a box (or a line)
- electrons are shown as arrows (↑ and ↓ represent electrons with opposite spins)
Example - Oxygen ( z = 8 )

Orbital Diagram Principles:
Aufbaul Principle: Electrons fill the lowest energy orbitals first.
Pauli's Exclusion Principle: Each orbital holds a maximum of 2 electrons with opposite spins.
Hund’s Rule: Within a sublevel, one electron occupies each orbit before any orbital gets a second electron.
Exception to the Aufbaul Principle:
Exceptions (more stability with half/full-filled sub-shells):
Cr: [Ar] 4s¹ 3d⁵
Cu: [Ar] 4s¹ 3d¹⁰
When forming ions, 4s electrons are lost before 3d.
1.3.6 & 1.3.7 : Ionisation Energy (HL)
Ionization Energy (IE) is the amount of energy required to remove one mole of electrons from one mole of gaseous atoms or ions in their ground state.
X(g) →X (g) + e
+
-
Measured in kilojoules per mole (kJ/mol)
Ionisation Energy Trend:
Across a Period (→): IE generally increases across a period from left to right.
Due to increasing nuclear charge and decreasing atomic radius, making electrons harder to remove.
Down a Group (↓): IE decreases down a group.
Despite increased nuclear charge, the outer electrons are further from the nucleus and experiencemore shielding, making them easier to remove.
Discrepancies in the Ionization Energy Trend

Despite general trends, there are notable dips in certain places due to electronic structure:
Group 2 → 3 (e.g, Be → B)
Electron in Group 3 is in a p-orbital, which is slightly higher in energy than the s-orbital in Group2. It is easier to remove a 2p¹ electron than a 2s² electron. Therefore, B has a lower IE than expected.
Group 15 → 16 (e.g., N → O)
In Group 15, p-electrons are unpaired (e.g., 2p³ in nitrogen). In Group 16, an electron must pair up (e.g., 2p⁴ in oxygen), causing increased repulsion, making it easier to remove one. Hence, oxygen has a lower IE than nitrogen, despite a higher nuclear charge.
The Key Idea:
To sum it up: It requires more energy to remove each successive electron, especially once you begin
removing core (inner shell) electrons. A large jump in IE suggests an electron is being removed from a more stable, inner shell, often used to determine group number of an element.
Calculating Ionization Energy:
To calculate ionization energy we use the idea that energy of a photon can eject an electron if it meets or exceeds the required ionization energy. General formula we use to calculate IE:
IE = E x Na
1000
E is from the photon energy above
Na = Avogadro’s number = 6.022×10 mol
Higher Level
Application
Pull Up your Calculators, Data Booklets and Brains
Formulas & Constants Needed (Section 1&2 of the data Booklet )
Speed of Light (C) = 3.00 × 108 m s−1
Planks Constant (h) = 6.63 × 10-34 J s
Avogadros Constant (Na) = 6.022 × 1023 mol-1
Worked Example:
The minimum energy required to ionize a hydrogen atom is provided by a photon with a wavelength of 9.50 × 10−8 m. Calculate the ionization energy of hydrogen in kJ/mol.
Solution:
E = (c x h)
λ
E = (3.00 x 108 m/s) x (6.63 x 10^-34 J s)
9.50 x 10^-7 m
E= 2.10 x 10^-18 J
IE = E x Na
1000
IE = (2.10 x 10^-18 J) x (6.022 x 10^23)
1000
IE = 1265 kJ/ Mol
